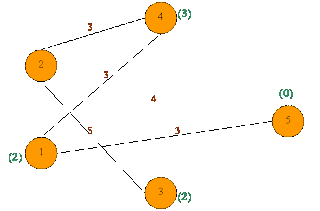
Suppose the following graph is drawn showing interconnected cities. It is a two way graph. A person can move in any direction like from vertex 2 to vertex 4 or from vertex 4 to vertex 2. An edge tells the distance between two connected cities. Different search algorithms use different strategies to find the path from source node to destination node.
Figure 4(a)
Best First Search
Best First Search is abbreviated as BEFS. It is an informed search. It uses heuristic function (i.e. estimated value to reach from a given node to goal node) to find the shortest distance from source node to destination node.
Suppose for above drawn graph (figure 4(a)) showing connected cities
Source node – 2
Destination node – 5
1. We need to add heuristic value to each node. Heuristic value is the estimated value to reach from a given node to the goal node. It should be less than or equal to actual distance. Heuristic values added to each node for destination node 5 is shown below in figure 4(b).
Figure 4(b)
2. Source Node is Node 2. On pressing any key, it is highlighted with another round of red colour as shown in figure 4(c).
2. Source Node is Node 2. On pressing any key, it is highlighted with another round of red colour as shown in figure 4(c).
Figure 4(c)
3. Child nodes or connected nodes to Node 2 are Node 4 (heuristic value 3) and Node 3 (heuristic value 2). Node 3 is having less heuristic value so it explores next as shown in figure 4(d). Although actual distance to reach Node 3 is more than distance to reach Node 4 but it does not consider actual distances at all.
Figure 4(d)
4. It does not consider visited nodes again. Like for Node 3, Child nodes are Node 2 (heuristic value 4) and Node 4 (heuristic value 3). Here heuristic value of Node 4 is less than heuristic value of Node 2, so it is explored next as shown in figure 4(e). Suppose even if heuristic value of Node 2 is less, still it will consider Node 4 because Node 2 is visited node.
Figure 4(e)
5. Node 4 has two child nodes Node 1 and Node 3. Here both Node 1 and Node 3 are having same heuristic value with value 2. But Node 3 is already visited node, so Node 1 will be visited next.
Even if there are two unvisited nodes having same heuristic value, then it works in increasing order. Node lesser in number will explore first. Suppose there are two unvisited nodes Node 2 and Node 4 having same heuristic value, Node 2 will be explored than Node 4.
So here next visited node is Node 1 as shown in figure 4(f)
Figure 4(f)
6. Node 1 has child nodes Node 4 and Node 5. Node 5 is having 0 heuristic value, which shows it is destination node. So it is next visited node as shown in figure 4(g)
Figure 4(g)
Hence Destination Node 5 is found. So search is complete.
Best First Search finds the solution in very less time. But we can see from above search that solution found is not always optimal. Path searched by Best First Search to reach from source Node 2 to destination Node 5 is 2 -> 3 -> 4 -> 1-> 5; total actual distance is 5+4+3+3 = 15
For path 2 -> 4 -> 1 -> 5; total distance is 3+3+3 = 9 which is lesser than path found by Best First Search.
NB: The system displays the path from destination node to source node. It first checks for the shortest path route and then displays nodes in reverse direction.