Dijkstras Algorithm

Suppose the graph (figure 3(a)) is drawn showing interconnected cities. It is a two way graph. A person can move in any direction like from vertex 2 to vertex 4 or from vertex 4 to vertex 2. An edge tells the distance between two connected cities. Different search algorithms use different strategies to find the path from source node to destination node.

Figure 3(a)

Dijkstra’s Algorithm

Dijkstra’s Algorithm is a special form of Breadth First Search. Dijkstra’s Algorithm finds the shortest distance from the source node to the destination node. It is also known as Single Source Shortest Path. It can find shortest distance from a single source point or source node to any destination node. Like Breadth First Search, it also searches level by level for destination node. It looks for shortest distance from one node to another. It stores distance from any current node to source node, till it does not find destination node with shortest distance.

Suppose for above drawn graph (figure 3(a)) showing connected cities

Source node is 1
Destination node is 5

1. On pressing any key, Source Node 1 gets highlighted with red colour another circle as shown in fig 3(b).

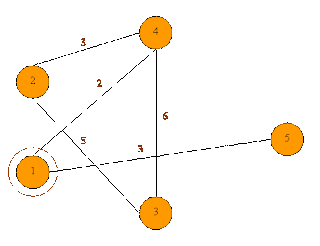
Figure 3(b)

2. Same as Breadth First Search, it looks for child nodes of parent node Node 1. Node 4 and Node 5 are child nodes of Node1. Node 5 is directly connected Node and there is no other way to reach Node 5. Hence this is the only and shortest distance to reach Node 5. So in Dijkstras Node 5 get explored next as shown in figure 3(c).

Figure 3(c)

Hence Node 5 is destination node. So Search is complete.

In Dijkstras Algorithm, it does not explore all nodes like in Breadth First Search. Only nodes which are used to reach from source node to destination node having shortest path are explored. It saves a lot of space.

NB: The system displays the path from destination node to source node. It first checks for the shortest path route and then displays nodes in reverse direction.